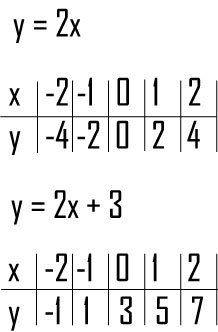Statistics

Our class ages (the data we will use as an example): 16, 15, 15, 15, 16, 16, 16, 16, 16, 15, 16, 16
This is a data set. It has some characteristics, we can use technology to learn some things about the data set.

For Instance:
1. Median (average)
"add all the numbers then devide by the number of numbers" ; )




2. Measures of Central Tendency
a) Median
The middle number, provided they are arranged numerically, and is odd (if n is even then the median is the mean of the two middle numbers).
b) Mode
"The most frequently appearing value." * There can be multiple modes or no modes.*

3. Range
The distance (in numbers) from the smallest to largest or vice versa (always positive).


How to get this information on you ti 83/84 calculator:

I. Clear your stat plots or be sure to use the correct plot when inserting you information (I'm using the information from the example at the begining of the post).
II. Go to "STAT" then "1: Edit..." and insert your list.
III. Go to "STAT", "CALC" then "1: 1-Var Stats".
IV.Now enter you list number (L1, L2, etc.). If your using our (class) example you should have first cleared all your lists and now on your home view (with 1-Var Stats on it) you will push "2nd, 1" to enter L1. "ENTER"

Vertical Line Test

Vertical Line Test

If a vertical line can be drawn to intersect more than exactly one point on a relation then that relation cannot be a function because it fails the vertical line test.

Relations and Functions

Relation is any set of ordered pairs.

ex) {(2,6),(-7,7),(4,3),(-7,2)}

X 0 1 2 3 4 5 6
Y 0 1 2 3 4 5 6

X--------M
Y--------N
Z--------O


y=2x+5
"the set of ordered pairs such that y is twice x"

all of these relations are functions except one. The first one isn't a function because it fails the vertical line test.

Regular Polygons

A regular polygon is when all the side lengths and angles are the same and don't intersect each other.

Equilateral Triangle

Number of sides = 3:
Number of vertices = 3:
Interior angle = 60°:
Exterior angle = 120°:
Exterior angle multiplied by the number of sides = 360°:
Number of sides = number of vertices:

Cube

Number of sides = 4:
Number of vertices = 4:
Interior angle = 90°:
Exterior angle = 90°:
Exterior angle multiplied by the number of sides = 360°. (90°X4=360°):
Number of sides = number of vertices:

Pentagon

Number of sides = 5:
Number of vertices = 5:
Interior angle = 108°:
Exterior angle = 72°:
Exterior angle multiplied by the number of sides = 360°. (72° X 5 = 360°):
Number of sides = number of vertices:

Hexagon

Number of sides = 6:
Number of vertices = 6:
Interior angle = 120°:
Exterior angle = 60°:
Exterior angle multiplied by the number of sides = 360°. (60° X 6 = 360°):
Number of sides = number of vertices:

Heptagon

Number of sides/verticies = 7

Interior angle = 128.57

Exterior angle = 51.53

Octagon

Number of sides/verticies = 8
Interior angle = 135

Exterior angle = 45

Nonagon

Number of sides/verticies = 9
Interior angle = 140

Exterior angle = 40

Decagon

Number of sides/verticies = 10

Interior angle = 144
Exterior angle = 36

3D Shapes/Prisms

Cube/Rectangular prismSphereRectangular Pyramid Triangular Pyramid
Cylinder
Cone

Octahedron (8 faces, 6 vertices, 12 edges)Dodecahedron (12 faces, 20 vertices, 30 edges)

Icosahedron (20 faces, 12 vertices, 30 edges)

Torus

2D Shapes

Triangle, Rectangle, Square, Cirlce,

Parallelogram

Trapezoid

Rhombus
Ellipse
Kite

Sector

Internet Radio

Hey, since Pandora's not streaming in Canada anymore I've found some other sites for free radio.

www.accuradio.com is awesome (I love da jazz).
www.allworship.com works with windows media player and is all christian.

www.live-radio.com and www.live265.com (you'll need a username and password for this one) both didn't work for me in the school but... there still there.

Cosine Law

In any triangle the sim of two sides squared less twice those two side lengths multiplyed by the cosine of the included angle yields the included side squared.

a^2=b^2+c^2-2bc(cosA)
b^2=a^2+c^2-2ac(cosB)
c^2=a^2+b^2-2ab(cosC)
You would use these three to solve for a line segment and these other three would be used for finding an angle.
cosA=a^2-b^2-c^2/-2bc
cosB=a^2-b^2-c^2/-2ac
cosC=a^2-b^2-c^2/-2ab

Sine Law/Law of Sines

In any triangle, if you compare the sine ratio of any angle to its corresponding side, the value is unique to that triangle, and can be used to find either the sine ratio of other angles or the corresponding other sides.

* You need to know at least a pair of corresponding angles/or sides and one other angle/side to make the law of sines visible.

ex) Angle A is 39 degrees, Angle C is 67 degrees and side a is 6.53. Solve the triangle.

sinA/a=sinR/r
sin39/6.532 = sin67/c
6.532(sin67)=sin39(c)
6.013/sin39=sin39(c)/sin39
9.554=c

Note: in the third step I cross multiplied.

Primary Trigonometry Functions

Sine (sin)
Cosine (cos) and
Tangent (tan)

The first thing that come to mind when I hear these is: equation. I like to define these as equations or formulas for solving specific angles or line segments in a right angled triangle. You can remember these things by remembering soh-cah-toa (so - ka - toe - ah, you'll find out what I means as I go through them).

Sine
The abbreviation for sine is sin (not sin like in you did something bad but, sin like a stop sign, you still pronounce it like sine). The equation/formula for this is sin('theta')=opposite/adjacent (don't worry I'll have examples). You can remember sine my remembering the soh in sho-cah-toa, meaning s=o/h so sine equals opposite divided by hypotenuse.

Cosine

The abbreviation for cosine is cos. The equation/formula for this is

cos('theta)=adjacent/hypotenuse. You can remember cos by remembering the cos in soh-cah-toa, meaning c=a/h so cos equals adjacent diveded by hypotenuse.

Tangent

The abbreviation for tangent is tan. The equation/formula for this is

tan('theta')=opposite/adjacent. You can remember tan by remembering the toa in soh-cah-toa, meaning t=o/a so tan equals opposite divided by adjacent.

ex) say we have a (right angled) triangle with the opposite as 3 and theta as 48degrees. Solve for adjacent.

tan'theta'=o/a

tan48=3/a

tan48(a)=3

tan48(a)/tan48=3/tan48

a=2.7012...

How Do You Learn Math Best???

Seriously, and further to our classroom discussion, when considering things like Accelerated Math, graphing calculators, computers, the internet, YouTube, wikis, podcasts, blogs, etc....Is it a wonder at all that students learn anything in my classroom? What works the best for you? Or... what suggestions do you have that may improve what we're doing on a day to day basis in class. Please be honest, but also please be respectful of the fact that we're in a learning environment...

This is and should be a conversation starter...so let's hear what your classmates have to say:

The Pythagorean Theorem

I know this is weird but, on Tuesday Mr. Max went and tried explaining what the Pythagorean Theorem really is. I found it incredibly boring, I was barely paying any attention - I was half asleep. I understood it was part of the curriculum to do this allover again, personally it barley made any sense to do so,(then again everyone isn't like me) so, I'm just gonna provide you with some websites that will give you a hazy look a what he did (I don't even know everything he did, I was surprised when he turned the light on, though mental math was fun! lol lol).

Proof of the Theorem
http://www.cut-the-knot.org/pythagoras/index.shtml
Java Applet
http://sunsite.ubc.ca/LivingMathematics/V001N01/UBCExamples/Pythagoras/pythagoras.html http://www.ies.co.jp/math/java/geo/pythasvn/pythasvn.html (I like this one, I like puzzles)
http://oneweb.utc.edu/~Christopher-Mawata/geom/geom7.htm (I think this one is the easiest to understand)

Pythagorean Triples
http://www.math.uic.edu/~fields/puzzle/triples.html
http://www.cut-the-knot.org/pythagoras/pythTriple.shtml

Oh, he also went on about who Pythagoras is. LoL, I'm reading a book about astronomy right now and I happened to be reading a section about Pythagoras, I found he became quite insane (my personal opinion again). If anyone wants the details SEND ME AN EMAIL (semba04@mts.net or semba04@gmail.com) I'd love to share it with you, though I might post it anyway (on some boring day) (because I find that stuff extremely interesting).

Ah, yes. We also programed our calculators and spreadsheets to calculate the hypotenuse of a right (angled) triangle (which I found fun, again my opinion).

Wiki Assignment Rules

Wiki Assignment

1. Your assignment goes on: ___________________ , use the password on the whiteboard, but please leave the password out of your scribe posts.
2. You're essentially teaching someone how to do a 'type-problem' from Accelerated Math, from start to finish. Show the entire problem, the objective, any relevant instructional materials, whatever....and I believe that I said in class that it should be something you struggled with yourself, but that you're competent with now.
3. Remember that once a question/objective has been selected, it's not available for anyone else's assignment. Check carefully before you post.
4. It's a wiki, so SAVE YOUR CHANGES every time you make some changes....works in progress are fine, but there will be a final due date: .
5. No last names/identifiers in your posts...We've talked about this in class...please remember to be 'mostly anonymous'....

Standard Form Linear Equation

Ax+By+C=0

"A" and "B" are both coefficients of x and y. "C" is a constant term (just a number).

application: Solve for y:
Ax+By+C=0
By=-Ax-C
y=(-Ax/B)-(C/B)

y=mx+b
Therefore we see that m=-A/B and b=-C/B

Parallels and Perpenducilars

Parallel - two lines (rays, segments) are parallel if they are COPLANAR and EQUIDISTANT throughout their length.

Coplanar - A set of points is said to be coplanar if and only if they lie on the same geometric plane.
Equidistant - Equally distant. For example, any two points on a circle are equidistant from the center.

Perpendicular - two lines (rays, segments) are perpendicular if they are COPLANAR and Intersect at a 90 "degree" angle.

Point Slope Form

y-y1=m(x-x1)

Where m=slope & (x1,y1) corresponds to specific points on the coordinate
example: Consider the line 2x+3 and write its equation in point slope form
Graph the line: y=2x+3
Slope=2
Y-Intercept=3
x__________y
-1_________1
0__________+3
-2_________-1


y-y1=m(x-x1)
y-1=2(x-(-1)) or in simplified form y-1=2(x+1)
OR
y-3=2(x-0) or in simplified form y-3=2x
OR
y-1=2(x-(-2)) or in simplified form y+1=2(x+2)

Slope y-Intercept Form

y = mx + b
m is slope and b is y-intercept.

ex) Write the slope y-intercept form for the points (-2, 1) and (4, 4).

First find slope
= (y2 - y1)/(x2 - x1)
= (4 - 1)/(4 - (-2))
= 3/6
= 0.5 or 1/2

Now that we have a y-coordinate, the slope and an x-coordinate we can find the y-intercept.
b = y - mx
b = 4 - .5(4)
b = 4 - 2
b = 2

y = 0.5x + 2

http://www.gomath.com/exercises/SlopeEquationYintercept.php
http://www.learningwave.com/lwonline/algebra_section2/yintercept2.html
http://en.wikipedia.org/wiki/Linear_equation

Midpoint

Midpoint - A point on a line segment that divides the segment into two congruent segments. A point that is exactly half way between two set points.

http://library.thinkquest.org/20991/geo/coordgeo.html#distance

Distance

Distance - In the mathematical subfield of graph theory we can define a notion of distance between two vertices in a graph. The extent or account of space between two objects or points.

Find the distance between
A(-2, 3) and B(8, -1).

d = SQRT[(8 - (-2))^2 + (-1 - 3)^2]

Simplify.

d = SQRT[(10)^2 + (-4)^2]
d = SQRT(100 + 16)
d = SQRT(116)
d = 10.77units



http://library.thinkquest.org/20991/geo/coordgeo.html#distance

Slope

Slope - In mathematics, the slope of a straight line (within a Cartesian coordinate system) is a measure for the "steepness" of said line. With an understanding of algebra and geometry, one can calculate the slope of a straight line; with calculus, one can calculate the slope of the tangent to a curve at a point.

http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut15_slope.htm

Table of Values

Zooms

1) ZBox -allows you to draw a box to define the viewing window.
2) Zoom In -magnifies the graph around the cursor.
3) Zoom Out-displays more of the graph around the cursor
4) ZDecimal- sets the change in X and Y to Increments of 0.1 when you use trace
5) ZSquare- Adjusts the viewing window so that X and Y dimensions are equal
6) ZStandard- Sets the standard (default) window variables
7) ZTrig- Sets the built in Trigonometry window variables
8) ZInteger- After you position the cursor and press Enter, sets the change in X and Y to whole number increments
9) Zoom Stat- Sets the variables for currently defined statistical lists
0)Zoom Fit-Fits Y-min and Y-max between X-min and X-max

Domain and Range

Domain -all real numbers (x1,x2=infinity)
Range -all real numbers (y1,y2=infinity)

Example: find the range of the relation in the arrow diagram?
3 -- 9
-6 -- 2
5 -- 10

R= {9,2,10}
and the Domain would be D={3,-6, 5}

This is a graph of y=2-x
the x-intercept is at (2,0) and the y-intercept is at (0,-2)

d={" all real numbers"}

r={"all real numbers"}

MODE

Numeric Notation
- Normal
- Sci (scientific)
- Eng (engineering)

Decimal
- Float: lets the number of the decimal place change based on the result (up to 10 digits)
- 0-9: Sets the number of decimal places to a value that you specify

Angle of Measure
- Radian: intercepts angle values as radians
- Degrees: Intercepts angle values as degrees

Type of Graph
- Func (functional): plots functions, where Y is a function of X
- Par (parametric): plots functions were X and Y are functions of T
- Pol (polar): plots functions where r is a function of [n] "theta"
- Seq (sequence): plots sequences

Sequential: draws graphs one at a time
Simul (simultaneous): draws several graphs at one time

Real or Complex mode
- Real: displays real numbers
- a+bi (rectangular complex): displays as 3+2i
- re^"theta"i (polar complex): displays as re^"theta"i

Screen Display
- Full: displays full screen
- Horiz: displays a horizontal split screen
- G-T: displays vertical split screen

Plot/Linear Regression

Plot
Method: Collect/Gather data. Determine which data might be dependent on the other.
ex) hours studied vs. test scores. Test score depends on hours studied.
Dependent Variable (y-axis, L2), Independent Variable (x-axis, L1)



You plot these points on your calculator by pushing STAT, Edit... Under L1 you put the hours studied and under the L2 you put the test score. To see your graph you push GRAPH.
If your graph doesn't appear push Y= and turn on Plot1.

Line of Best Fit (Linear Regression)
After plotting your points you can "see" the line of best fit by pushing:
STAT, CALC, 4:LinReg (ax+b), ENTER, 2nd, 1(L1), "comma", 2nd, 2(L2), "comma", VARS, Y-VARS, 1:Function, 1:Y1, ENTER, ENTER, GRAPH

To see the equation go to Y=

Simplifying Radicals (perfect squares)

1. Find the largest perfect square
SQRT (48) = 16

2. Write as the product of the perfect squares
SQRT (16 * 3) then SQRT(16)SQRT(3)

3. Reduce the "perfect" radical
SQRT(16)SQRT(3) = 4SQRT(3)

REDUCE: 3SQRT(50)
3SQRT(25 * 2) then 3SQRT(25)SQRT(2)
3*5SQRT(2) = 15SQRT(2)

Inequalities (Graphing in 1-D)

-Flip the inequality sign only when multiplying or dividing by negatives.

-open circle = greater/less than

-closed circel = equal to and greater/less than

-solve inequality as if solving a "regular" equation (with an equal sign)

ex) http://webgraphing.com/examples_inequality_1d.jsp

Number Sets

Natural N = {1, 2, 3...}
Whole W = {0, 1, 2, 3...}
Integer I = {... -2, -1, 0, 1, 2...}
Rational Q = {a/b; a, b "in the set" I, b "is not equal to" 0}
Decimal must terminate
Irrational IQ = Not in the set of Q
Real R = Q "and" IQ


The second diagram wasn't included in the lesson but, It has examples of N, W, I, Q, IQ, and R numbers.

First Post!

So we watched the slideshow that Mr. Kuropatwa in Winnipeg put together, and here's the first post that I'd like you to respond to:

1. What did you think of the video? What are your thoughts and comments?

2. What's it going to take? (I'll explain more about this in class...)


As usual, check back often, post freely but responsibly, and enjoy using the learning environment that you're creating for each other

RM